Fascynujące połączenia matematyki i przyrody

Świat roślin i zwierząt fascynuje naukowców, artystów, architektów, a nawet matematyków już od wielu stuleci. Niemalże od zawsze wiedziano, że natura skrywa w sobie tajemnice, które są warte odkrycia. Wiele inspiracji i projektów architektonicznych, artystycznych powstało dzięki natchnieniu pochodzącemu z obserwacji roślin. Już w czasach starożytnych znano geometryczne i arytmetyczne zależności w świecie roślin, a to skłoniło ludzkość do jeszcze wnikliwszego przyglądania się naturze. Dzisiejszy blog poświęcony jest fascynującej fuzji matematyki i przyrody, dzięki której możemy między innymi dostrzegać piękno tego świata.

CIĄG FIBBONACIEGO

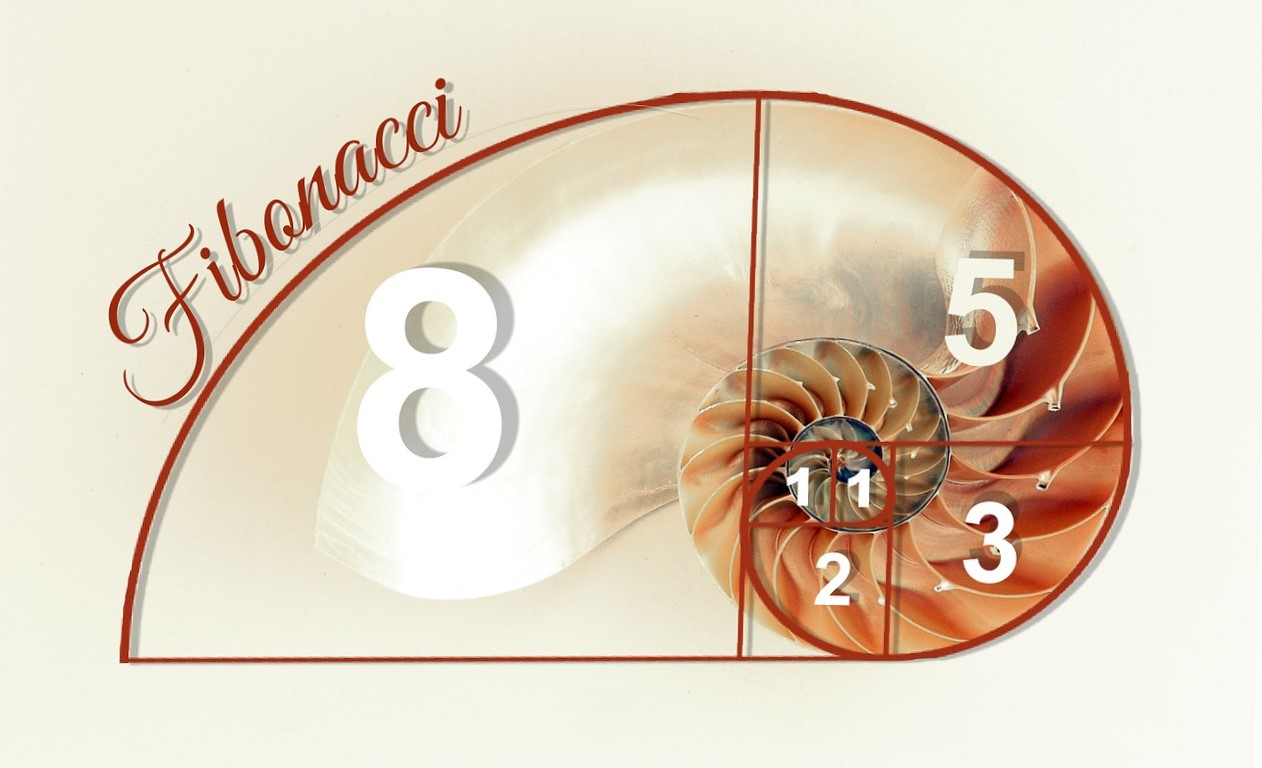
W roku 1202 włoski matematyk - Fibonacci (Leonardo z Pizy) odkrył matematyczny ciąg, który wyjaśnia proporcje w budowie wrzechświata, roślin, zwierząt i nas ludzi. Okazało się, że ciąg jest trafnym spostrzeżeniem. Jak to się stało? Nasz bohater zastanawiał się nad problemem rozmnażania królików: ile królików będzie mieściła klatka po upływie roku, jeśli z założenia każda para królików co miesiąc spłodzi nową parę, a ta zaś będzie mogła być reproduktywna po kolejnym miesiącu? Liczby Fibonacciego są przykładem rekurencyjnego ciągu liczb całkowitych, z którego wynika wiele zaskakujących własności matematycznych. Nie jest to bynajmniej coś skomplikowanego: jest to specyficzny ciąg liczb naturalnych, w którym każdy kolejny wyraz jest sumą dwóch poprzednich. Jeśli mielibyśmy przedstawić to na liczbach, wyglądałoby to następująco: 

0 +1 =1,
1+1 = 2,
1+2=3,
2+3=5,
3+5=8
5+8=13,
8+13=21....
I tak dalej. Ciąg ten jest nieskończony, a ilość jego wyrazów nieograniczona.

ZŁOTA PROPORCJA (BOSKA PROPORCJA)

Jedną z unikatowej zależności ciągu Fibonacciego jest stosunek każdego kolejnego wyrazu do poprzedniego. Dzieląc przez siebie kolejne dwa dowolne wyrazy ciągu otrzymamy stosunek, który w przybliżeniu wynosi 1,618. Im wyrazy o większej wartości, tym stosunek ten zbliżony jest bardziej do wartości 1,618. Wartość tą oznacza się grecką literą φ („fi”).

21:13=1,615
34:21=1,619
55:34=1,617
89:55=1,618……

Stosunek ten nazywany jest złotą bądź boską proporcją. Będąc w tym miejscu możemy w końcu przejść do wspomnianego wcześniej fascynującego połączenia matematyki z przyrodą. Weźmy chociażby do ręki muszlę ślimaka. Jej kształt układa się w regularną spiralę. To samo można powiedzieć o ziarnach słonecznika czy różyczkach kalafiora. Możemy zauważyć tutaj podobną zależność. Budowa galaktyki czy obraz z lotu ptaka cyklonu nie jest odosobnionym przykładem. Tak naprawdę jest ich mnóstwo. Ma w tym wszystkim swój udział boska proporcja, na której opiera się tzw. spirala Fibonacciego znana również pod nazwą złotej spirali. Jej szerokość zwiększa się bądź zmniejsza o 90 stopni φ razy. Innymi słowy kąt ten zmienia się o wartość boskiej proporcji, czyli w przybliżeniu 1,618. Żeby jeszcze bardziej zobrazować budowę spirali Fibonacciego, można powiedzieć, iż jest ona zbudowana z ćwiartek okręgów, gdzie dla każdej kolejnej jej promień to kolejny wyraz ciągu Fibonacciego.

Przyglądając się roślinom możemy zauważyć, że łodygi, liście czy kwiaty, rozwijające się z centralnie usytuowanych komórek wzrostowych (merystemów), dalej pojawiają się i rosną w kierunkach innych, jednakże zawsze pod pewnym kątem w stosunku do miejsca, z którego wyrosły pierwotnie.  Przy głębszym spojrzeniu staje się oczywisty fakt, iż rosną one na planie niewidzialnej spirali Fibonacciego. Ten kąt to kąt środkowy oparty na mniejszym z dwóch łuków powstałych w wyniku złotego podziału okręgu i nazywany jest "złotym kątem". I tak każdy kolejny kwiat czy liść pojawia się w miejscu wyznaczonym w oparciu o złoty podział. W rezultacie możemy obserwować uporządkowanie, czy to w kwiatostanach, ulistnieniu (spiralna filotaksja) czy nawet w pogodzie. Jak myślicie, dlaczego wir wodny wygląda tak, a nie inaczej? A czy zaskakujący będzie dla Was fakt, że nawet trasa lotu owada do źródła światła oparta jest na złotej spirali? Bardzo ciekawa jest również liczba płatków kwiatów poszczególnych gatunków roślin. O ile w trakcie rozwoju nie wystąpi żadna mutacja, ilość tych płatków jest stała i tak np. dla wilczomlecza wynosi 2, dla irysa 3, dzikiej róży 5, ostróżki 8 czy nagietka 13. Są to kolejne liczby z ciągu Fibonacciego. Bardzo dużo gatunków drzew cechuje się również spiralnym rozmieszczeniem gałęzi wokół pnia. Warto przyjrzeć się także szyszkom drzew iglastych, tam również odnajdziemy spiralę. Nawet nasze DNA zbudowane jest zgodnie z boską proporcją. 34 miary długości na 21 miar szerokości - są to, rzecz jasna, kolejne wyrazy ciągu Fibonacciego, i tyle właśnie mierzy cząsteczka DNA dla każdego odcinka podwójnej spirali.


CIEKAWOSTKA: Nasze logo również ukrywa w sobię zasadę złotej proporcji :)